Математический фундамент
Мы хотим рассказать Вам историю, которая, надеемся, покажет многообразие математики и ответит на вопрос, почему же её всё-таки нужно изучать.

Многим не нравится математика из-за её оторванности от реального мира: как в жизни может помочь стереометрия? Физика, химия и биология же являются чем-то реальным: с гравитацией, током и электромагнитными волнами мы имеем дело каждый день, а химию и биологию можно найти в собственном теле. А зачем же нужна математика? Почему некоторые посвящают ей свою жизнь?
Для многих учёных математика и выделяется тем, что не имеет какой-то особой связи конкретно с нашей вселенной, где есть определённые правила, определённые физические константы. Вместо этого, математика связана со всеми вселенными одновременно.
Мы хотим рассказать Вам историю, которая, надеемся, покажет многообразие математики и ответит на вопрос, почему же её всё-таки нужно изучать.
Где же начинается математика?
Для начала, начало мы будем искать не хронологическое, а больше идеологическое. Если все объекты реального мира состоят из атомов, то из чего состоят математические объекты? Что является математическими атомами? Как объединить три основных раздела математики (топологию, алгебру и функциональный анализ) под одной крышей?
Кантор, Фреге и Гильберт были одними из тех, кто пытался ответить на этот вопрос. Создать фундамент для всей математики, свод правил, который будет универсальным и достаточным.

Начнём с того, что математика в каком-то смысле не единственна: существует множество её вариаций. То, чем мы пользуемся сейчас, построено на конкретных аксиомах — утверждениях, которые считают истинными без доказательств. Из этих аксиом после и вытекают все теоремы, которыми мы пользуемся.
Так, например, все встречались в школе с аксиомами планиметрии, которые корнями уходят ещё во времена Евклида. Но он не единственный, кто пытался формализовать геометрию на плоскости: свои системы аксиом предлагали Давид Гильберт, Альфред Тарский и другие. Но не будем забегать вперёд. Как же это всё вообще началось?
Сомнения появились в XIX веке. Тогда математики начали более тесно работать с бесконечностью, что порождало разные противоречия и несостыковки. Кроме того, математический мир обнаружил «новую геометрию», пересмотрев пятый постулат Евклида о параллельных прямых.
Пятый постулат гласит, что в плоскости через точку, не лежащую на данной прямой, можно провести одну и только одну прямую, параллельную данной.
Лобачевский в своих работах предположил, что эта аксиома неверна. Вышло так, что из этого рождается совершенно новая, но тоже рабочая система со своими теоремами и утверждениями — геометрия Лобачевского (одна из неевклидовых геометрий).
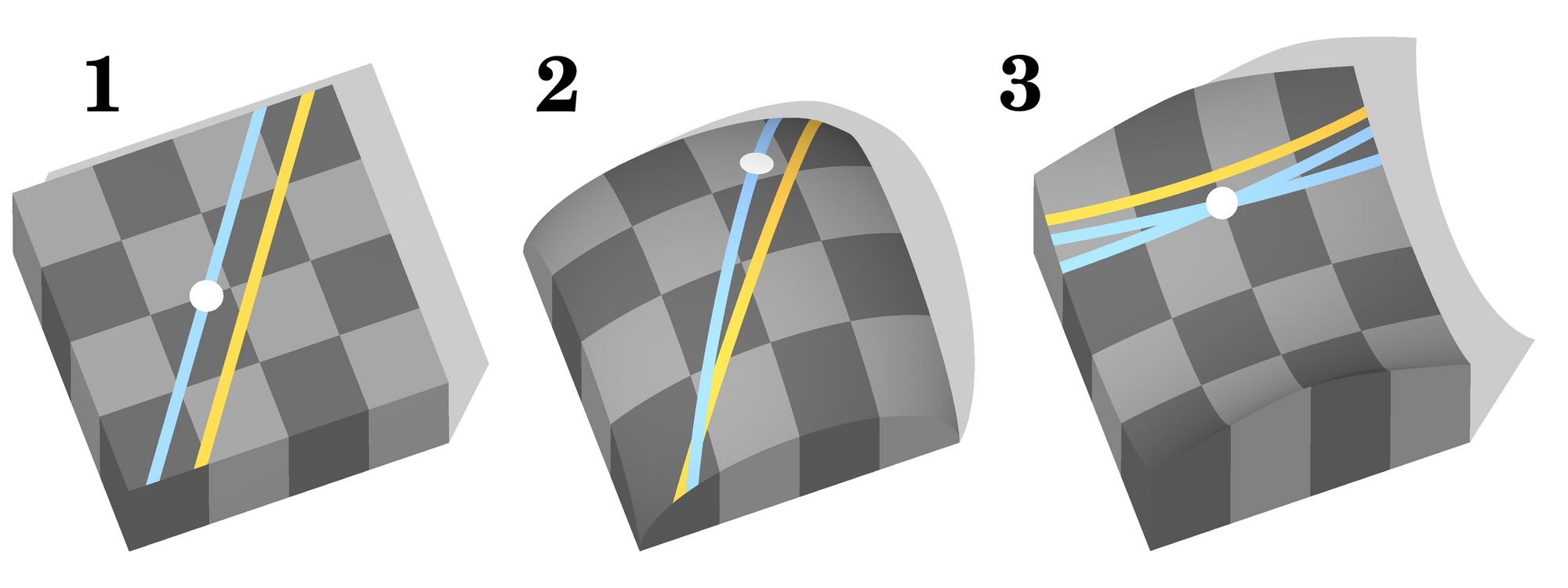
Это и некоторые другие события привели к серьёзному математическому кризису. К началу 20 века сформировались целые лагеря учёных, грезящих о построении устойчивого фундамента для всей математики: приверженцы формализма и логицизма.
Формализм – один из подходов к философии математики, пытающийся свести проблему оснований математики к изучению формальных систем. Грубо говоря, приверженцы формализма хотели задать все понятия чёткими и строгими формулами и символами, абстрагируясь от смысла используемого языка.
Логицизм – другой подход к философии математики, пытающийся свести всё к понятиям математической логики.
Приверженцы формализма и логицизма пытались объединить под одной крышей и алгебру, и геометрию, и исчисление, а также многие другие на первый взгляд абсолютно разные разделы математики.
Начало теории множеств
И одни из самых главных и серьёзных первых шагов на пути к этому удалось сделать Георгу Кантору благодаря разработанной им теории множеств.
Множество – набор каких-то предметов. Да, всё так просто. Предметы, входящие в множества, называются его элементами. (Да-да, круги Эйлера это визуализация множеств)
Теория множеств позволила формализовать арифметику и дала большие надежды на создание той самой нужной основы. Теория множеств ответила на многие вопросы, касающиеся бесконечности и позволила математикам общими словами говорить о самых различных объектах, таких как числа и фигуры. С помощью понятий теории множеств на сегодняшний день можно определить практически все математические объекты. Но путь был тернист.

Парадокс Рассела.
Уже в самом начале XX века была обнаружена проблема: парадокс Рассела.
Он достигается благодаря следующим фактам из Канторовской теории множеств:
(a) Множество может содержать само себя
(b) Можно сконструировать любое множество
Парадокс Рассела чем-то похож на парадокс лжеца, давайте с ним познакомимся:
1) Раз нам можно создавать любые множества, давайте создадим одно особенное. В наше множество будем добавлять только те множества, которые не содержат сами себя. Множества, не содержащие сами себя, далее будем называть обычными.
2) Давайте посмотрим, кто нам подходит.
Множество всех чисел нам подходит, потому что множество вещественных чисел не содержит само себя, оно содержит только числа: 1, 2, \(\pi\), \(e\) и так далее. Множество вещественных чисел является обычным.
Множество всех множеств нам не подходит, потому что чтобы содержать все множества, оно должно содержать и себя, а такого нам не надо. Множество всех множеств не является обычным
А еще нам подходит множество, содержащее только обычные множества. Такое множество является обычным.
3) Теперь спросим: а будет ли множество обычных множеств содержать саму себя?
Допустим, наше множество содержит само себя. Тогда оно не является обычным, а раз не является обычным, то и в нашем множестве содержаться не должно. Получили противоречие.
Хм, ну пусть тогда наше множество не содержит само себя. То есть оно обычное. Но если оно обычное, то мы должны добавить его в наше множество. Снова противоречие!
Странно, парадокс какой-то.
Вот именно! Это он и есть.
Но ты ведь знаешь много парадоксов, читатель. Парадокс Монти Холла, парадокс Зенона об Ахиллесе и черепахе. Они же прикольные и безобидные, разве нет? Не совсем.
Для математиков обнаружение парадокса в рамках какой-то теории означает наличие ошибки, несостыковки в аксиомах этой теории. Никому ведь не хочется выводить, что какое-то утверждение одновременно правдивое и ложное. Это вам не квантовая физика!
Пост-парадоксальная эра: Рассел.
Теперь, чтобы понять, с каким энтузиазмом некоторые умы старались построить фундамент для математики, давайте посмотрим на дальнейшие действия Бертрана Рассела после обнаружения им вышеописанного парадокса.

Чтобы исправить несостыковки теории множеств Кантора, Рассел и Уайтхед начали разрабатывать свою — теорию типов, в которой множества подразделялись на классы. Эта теория позволяла обойти парадокс Рассела, но какой ценой? Авторы теории почти 10 лет работали над книгой по ней и по несколько раз всё переписывали, а в процессе ушли в такие дебри, которые заставили многих математиков сомневаться в разумности такой системы.

Пост-парадоксальная эра: Цермело.
Но математика не стояла на месте. В то же время Эрнст Цермело решал ту же проблему — пытался создать новые "удачные аксиомы". Благодаря ему и дальнейшим улучшениям его теории математиками Абрахамом Френкелем и Туральфом Скулемом, на свет появилась аксиоматика ZF, на которой математика стоит до сих пор.

30 лет ушло на построение самых базовых правил математики. Объединёнными усилиями наконец удалось устранить неприятные парадоксы первоначальной вариации теории множеств.
Гёдель и "Теорема о Неполноте"
Но путь ещё не был окончен, у математиков ещё оставались вопросы о некоторых свойствах математики как системы: полна ли и непротиворечива ли математика? С этими вопросами миру помог разобраться Курт Гёдель с его великой Теоремой о Неполноте.

Разберёмся сначала, что означают полнота и непротиворечивость. Это два очень важных концепта, позволяющих описать систему.
1) Полнота системы означает отсутствие в ней утверждений, которые нельзя доказать. Другими словами, в полной системе всегда можно доказать или опровергнуть любое корректное предположение.
2) Непротиворечивость системы, как ни странно, означает отсутствие в системе противоречий. В непротиворечивой системе невозможно доказать, что какое-то утверждение является одновременно и истинным, и ложным.
Математика долгие века считалась полной и непротиворечивой системой, но Гёделю удалось разрушить построенный в головах математиков воздушный замок. Сначала он доказал, что в математике всегда будут присутствовать недоказуемые истины. Чуть позже выяснилось, что если система и является непротиворечивой, то это всё равно невозможно доказать, пользуясь инструментами, которые эта система предлагает.
Таким образом, оказалось, что всё куда запутаннее и интереснее.
Что тогда делать?
Что, если, например, на пути математиков встретится очень важное утверждение, без доказательства которого дальше продвинуться просто невозможно, и оно окажется недоказуемым? Тогда всё кончено?
Не совсем, ведь систему аксиом всегда можно дополнить и сделать математику ещё более сильной системой, в которой уже можно будет продвинуться дальше. Но добавлять новые аксиомы, конечно, нужно очень аккуратно. Необходимо следить за тем, чтобы они не противоречили прошлым и не ломали никакие существующие концепты.
На самом деле, внедрение новой аксиомы происходит и сейчас. Частью математического мира стала Аксиома Выбора, позволяющая делать больше интересных вещей с бесконечностью, а именно выбрать из бесконечного количества множеств по одному элементу. Нельзя сказать, что она прямо «официально» считается аксиомой, потому что не все математики её принимают, но сегодня на неё активно ссылаются при доказательстве многих интересных результатов.
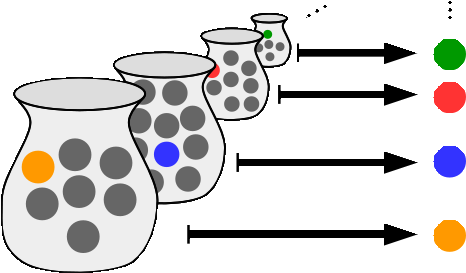
Альтернативная математика
Более того, мы можем не просто добавлять новые аксиомы, мы можем строить совершенно противоположные «рабочие» миры. Так произошло с Континуум-гипотезой (грубо говоря, вопросе о существовании чего-то среднего между счётной и несчётной бесконечностями, углубляться в детали не очень важно): было доказано, что к существующая математика будет работать и если Континуум-гипотезу считать верной, и если считать её неверной. То есть мир может выбрать, по какой дороге ему дальше идти, ведь Континуум-гипотеза существует независимо от нашей науки о числах, функциях, множествах и многом другом.
Вывод
Так, работа по исследованию азов математики позволила будущим поколениям по-другому взглянуть на науку. Рамки были сдвинуты и теперь у математиков есть куда больше свободы. Появилось осознание, что все системы — конструкции, начальные параметры которых пользователь выбирает сам.
Математика всегда в каком-то смысле была магазином инструментов, куда приходили физики, химики, биологи, экономисты, чтобы найти что-то нужное и удобное. Например, комплексные числа ждали своего часа несколько сотен лет. Они впервые упоминаются математиком Кардано в 1545 году, а активно использоваться для решений физических проблем, связанных с гидро- и аэродинамикой, переменным током, они начали только в 19 веке. Тогда учёные были ограничены только одним отделом в математическом магазине. Сегодня же благодаря кропотливой работе многих математиков, можно посетить и другие, стоящие на изменённом фундаменте.
